








 2
2



































































































































 2
2

 2
2


 10
10 619
619 377
377

 44
44
 14
14



 5
5
 2
2



 29
29


 22
22

 2
2 2
2

 99
99 52
52 3
3 3
3 20
20 2
2
 8
8 5
5
 9
9 301
301 34
34 11
11 15
15 21
21


 9
9 52
52 7
7 6
6 10
10 3
3 80
80 357
357 122
122 4
4 2
2
 47
47 38
38 11
11 47
47 6
6 65
65 7
7 57
57 13
13 31
31 24
24 19
19 4
4 3
3
 2
2 3
3 489
489
 2
2 5
5 4
4 19
19

 3
3

 27
27 2
2 19
19 23
23 11
11 21
21
 195
195 10
10 3
3 3
3 2
2 15
15 4
4 463
463 38
38 49
49 11
11 7
7 19
19 6
6 4
4
 16
16
 4
4 42
42 8
8 3
3 12
12 14
14 3
3 24
24



 6
6 58
58






 22
22
 1496
1496 2
2 25
25

 35
35 11
11 22
22




 7
7В пазле из 4 тура у меня не хватает как минимум трех деталей. @Grandgames, посмотрите, пожалуйста
 2
2
@Grandgames, мне кажется, что в результатах этого турнира какой-то глюк. Победа была засчитана Dimmaric, хотя он не решил головоломку, мой турнирный рейтинг уменьшился. Посмотрите, пожалуйста.
 7
7
@GrandGames, пересмотрите, пожалуйста, концепцию кремния. Он слишком широко используется (например, при создании электроники), чтобы иметь настолько ограниченный шанс получения.
 8
8
@GrandGames, результаты кругового турнира опять некорректны. посмотрите, пожалуйста.
 3
3
В результатах опять что-то непонятное насчиталось. @Grandgames, посмотрите, пожалуйста.
 4
4
Уважаемый @Grandgames, после окончания турнира не отображаются игроки и результаты. Похоже, что проблема возникла только для этого турнира или только для турниров по круговой системе. Посмотрите, пожалуйста.
 5
5
@GrandGames, мне кажется, что в выбор картинки для медали турнира закрался баг. В этом турнире отображается мультисудоку вместо какурасу, в маяках - математические головоломки. Посмотрите, пожалуйста.
 4
4
Уважаемый @GrandGames, при формировании этого турнира произошла ошибка. Участников 13, а туров сформировалось 12. В результате каждый игрок (за исключением milutin03) не сыграл одну игру. Посмотрите, пожалуйста.
 4
4
Кажется, на сайте сломались турниры. Марафон должен был начаться 20 минут назад, но ничего не произошло. @GrandGames, посмотрите, пожалуйста.
 8
8
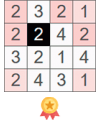
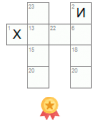
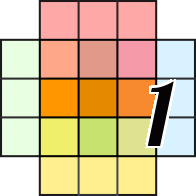
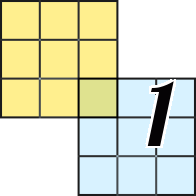
1. There is a cell with the number 0 highlighted in blue. This means that all adjacent empty cells can be marked as white (highlighted in blue).
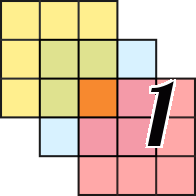
2. Let's consider a pair of adjacent cells containing the numbers 2 and 4 (highlighted in red). Both of these cells border the edge of the field. Consequently, each of these cells has six cells analyzed when calculating the number in that cell. Out of these six cells, four are common. Since one cell contains the number 2 and the other contains 4, two cells (highlighted in blue) adjacent only to the cell with the number 2 must be white, and those adjacent only to the cell with the number 4 (highlighted in green) must be black.
NB: At this stage, a pair of cells with numbers 2–4 is considered, but identical conclusions are drawn for pairs 1–3 and 3–5.
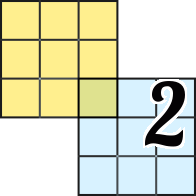
3. Let's consider a pair of adjacent cells highlighted in red and apply reasoning similar to point 2.
4. Let's consider a pair of adjacent cells containing the numbers 7 and 4 (highlighted in red). Each of these cells has nine cells analyzed when calculating the number in that cell. Six of these cells are common. Thus, three cells (highlighted in blue) adjacent only to the cell with the number 4 must be white, and those adjacent only to the cell with the number 7 (highlighted in green) must be black.
NB: At this stage, a pair of cells with numbers 7–4 is considered, but identical conclusions are drawn for pairs 8–5 and 6–3.
5. Let's consider a pair of adjacent cells highlighted in red and apply reasoning similar to point 4.
6. Cells with numbers highlighted in brown have appeared on the field. This means that all adjacent empty cells can be marked as black (highlighted in green).
7. As long as there are numbers highlighted in blue or brown on the field, it is necessary to color the adjacent empty cells as shown in points 1 and 6.
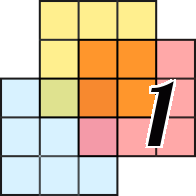
8. Let's consider a pair of adjacent cells highlighted in red. For the cell containing the number 4, three adjacent cells are colored black, so one of its six adjacent empty cells must be black, and the rest must be white. For the cell containing the number 6, also three adjacent cells are colored black, meaning three of its adjacent cells must be black, and three must be white. The considered cells have four common empty cells. Obviously, the only way to satisfy all conditions is to color black two cells adjacent only to the cell with the number 6 (highlighted in green), and color white two cells adjacent only to the cell with the number 4 (highlighted in blue).
9. Numbers highlighted in blue and brown appear on the field again. Empty cells should be colored similarly to point 7.
10. The puzzle is solved!
 12
12
Ссылка на первый тур ведет на страницу турнира. @GrandGames, посмотрите, пожалуйста.
 3
3
@GrandGames, посмотрите, пожалуйста, ссылка первого тура ведет просто на главную страницу.
 3
3
@Meduzia - @iris8
Воскресенье, 1 декабря, 15:00.
Список головоломок (5-10 мин):
 4
4
@GrandGames, у меня сегодня перестали работать горячие клавишы Alt+Q в полимино-паззлах. Насколько я понимаю, это баг.
 5
5
Как решать головоломку «Найди три»
Разбор головоломки https://en.grandgames.net/findthree/id449586
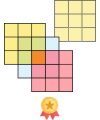
1. Сначала проанализируем форму всех фигур. Среди 12 фигур присутствует 5 кругов, 5 полуовалов и только 2 квадрата. По условиям головоломки форма всех трех фигур в группе либо одинакова, либо не повторяется. Единственный возможный вариант подобного разбиения данного набора фигур следующий: круг-круг-круг, полуовал-полуовал-полуовал, круг-полуовал-квадрат, круг-полуовал-квадрат.
 10
10
 6
6
 2
2
 7
7
 3
3
 9
9
 8
8
 8
8
 5
5
 4
4
 19
19
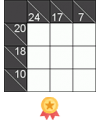
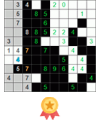
Разбор головоломки https://en.grandgames.net/walls/id389670
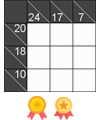
1. Рассмотрим клетку с числом 5 в левом верхнем углу (выделена красным). К ней примыкает два блока клеток, в которых можно провести линии (выделены синим). Однако для того, чтобы количество проходящих через эту клетку линий было равно 5, три клетки из вертикального блока должны обязательно содержать вертикальные линии (выделены зеленым).
2. Рассуждения, аналогичные пункту 1, применяются еще к 4 клеткам с числами (выделены красным). Блоки клеток, которые необходимо заполнить соответствующими линиями, выделены зеленым.
3. Рассмотрим клетку, выделенную синим. Если она будет содержать вертикальную линию, то количество линий, проходящих через выделенные красным клетки, будет не соответствовать числам в этих клетках. Следовательно, искомая клетка должна содержать горизонтальную линию.
4. Рассмотрим 4 клетки, выделенные красным. Для всех них остался единственный вариант заполнения примыкающих клеток, который позволит провести требуемое число линий через эти клетки.
5. После выполнения пункта 4 появились еще 2 клетки, для которых можно применить аналогичные рассуждения.
6. Появились еще 2 клетки с полностью определенными соседями.
7. Через клетку с числом 7, выделенную красным, уже проходит необходимое количество линий. Следовательно, клетка, выделенная синим, должна содержать горизонтальную линию.
8. Для 3 клеток с числами появились однозначно определенные блоки (аналогично пунктам 1 и 4).
9. Теперь аналогичные рассуждения можно применить еще к 2 клеткам.
10. К двум клеткам, выделенным синим, применяются рассуждения, аналогичные пункту 7. Таким образом, эти клетки должны содержать горизонтальные линии.
11. Для 4 оставшихся клеток с числами остался единственно возможный вариант заполнения примыкающих клеток.
12. Головоломка решена!
 16
16
 4
4
 3
3
